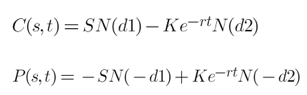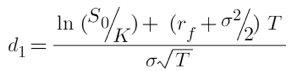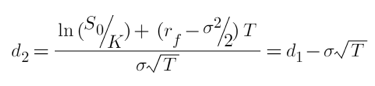Black Scholes Merton con Python

El método Black-Scholes de Merton para la valoración de opciones puede ser algo tedioso de calcular a mano aunque tenemos muchas herramientas gratuitas en internet para realizar este cálculo simplemente introduciendo los datos de las fórmulas.

He pensado que puede ser interesante disponer de una herramienta en Python para automatizar este proceso. Será necesario que instalemos la librería SciPy si no la tenemos.

pipenv install SciPy

En el artículo de las griegas resumimos las condiciones necesarias para poder aplicar el modelo correctamente y no veo necesario realizar una explicación del modelo otra vez.

En este artículo me limitaré a analizar el código y a explicarlo para que sea entendible. El código define un modelo BS sin dividendo.

def d1(S, K, r, Vol, T):
    return (np.log(S/K) + ((r + (Vol**2)/2) * T)) / (Vol* np.sqrt(T))
            
def d2(S, K, r, Vol, T):
    return (np.log(S/K) + ((r - (Vol**2)/2) * T)) / (Vol* np.sqrt(T))

def BSMCall(S, K, r, Vol, T):
    d_uno = d1(S, K, r, Vol, T)
    d_dos = d2(S, K, r, Vol, T)
    return (S*norm.cdf(d_uno)) - (K*np.exp(-r*T)*norm.cdf(d_dos))

def BSMPut(S, K, r, Vol, T):
    d_uno = d1(S, K, r, Vol, T)
    d_dos = d2(S, K, r, Vol, T)
    return (K*np.exp(-r*T)*norm.cdf(-d_dos)) - (S*norm.cdf(-d_uno))

La programación de las fórmulas es sencilla. Para d1 y d2 necesitamos conocer las variables que las componen: precio del subyacente (S), strike de la opción (K), la tasa libre de riesgo (r), volatilidad entendida como desviación estándar (stdev) y tiempo a vencimiento (T).

En el caso de las funciones BSM, necesitamos calcular N(x) con norm.cdf para la función de distribución acumulativa CDF(x).

assets = ['FB']

data = pd.DataFrame()
data = wb.DataReader(assets,data_source='yahoo', start='2020-1-1')['Adj Close']

log_returns = np.log(1+data.pct_change())
Vol = log_returns.std() * 252 **0.5

Este código ya lo conocemos de entradas anteriores.

Seleccionamos el último precio de cierre del subyacente (S), en este caso de $FB y calculamos los retornos logarítmicos a partir de 2020 hasta YTD.

Para el cálculo de la volatilidad necesitamos la desviación estándar de esos retornos log_returns.std() anualizada *252 y elevado a 1/2 (o raíz cuadrada sqrt()).

r = ""    #Risk free rate
K = ""    #Strike
T = ""    #Tiempo a vencimiento

Los parámetros libres del modelo. Debemos escoger discrecionalmente el valor de r en función del bono a 10 años estadounidense por ejemplo o tasas parecidas. El strike de la opción a valorar (K) , tiempo restante a vencimiento (T) y la tasa libre (r) son variables dinámicas que tendremos que introducir manualmente. El precio del subyacente se escoge a través de yahoo finance y el parámetro de la Volatilidad (Vol) viene de la desviación estándar de los resultados logarítmicos del periodo de resultados que escogemos a través del argumento start= y que finalizamos con end=, por ejemplo.
 

import numpy as np
import pandas as pd
from math import *
from pandas_datareader import data as wb
from scipy.stats import norm


r = 0.025    #Risk free rate en tanto por uno
K = 125      #Strike
T = 1        #Tiempo a vencimiento

assets = ['FB']
data = pd.DataFrame()
data = wb.DataReader(assets,data_source='yahoo', start='2020-1-1')['Adj Close']

S = data.iloc[-1]

log_returns = np.log(1+data.pct_change())
Vol = log_returns.std() * 252 **0.5

def d1(S, K, r, Vol, T):
    return (np.log(S/K) + ((r + (Vol**2)/2) * T)) / (Vol * np.sqrt(T))
            
def d2(S, K, r, Vol, T):
    return (np.log(S/K) + ((r - (Vol**2)/2) * T)) / (Vol * np.sqrt(T))

def BSMCall(S, K, r, Vol, T):
    d_uno = d1(S, K, r, Vol, T)
    d_dos = d2(S, K, r, Vol, T)
    return (S*norm.cdf(d_uno)) - (K*np.exp(-r*T)*norm.cdf(d_dos))

def BSMPut(S, K, r, Vol, T):
    d_uno = d1(S, K, r, Vol, T)
    d_dos = d2(S, K, r, Vol, T)
    return (K*np.exp(-r*T)*norm.cdf(-d_dos)) - (S*norm.cdf(-d_uno))

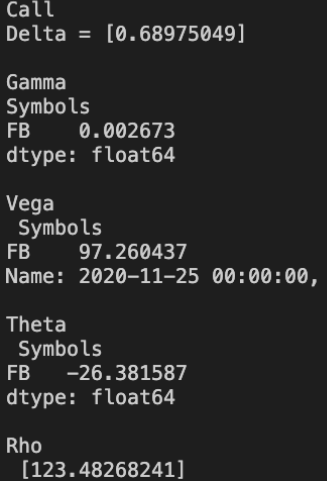
Podemos aproximar las derivadas parciales del modelo, también conocidas como las griegas.

En el caso de las opciones de compra:

def BSMCallGreeks(S, K, r, Vol, T):
    d_uno = d1(S, K, r, Vol, T)
    d_dos = d2(S, K, r, Vol, T)
    Delta = norm.cdf(d_uno)
    Gamma = norm.pdf(d_uno)/(S*Vol*sqrt(T)
    Theta = -(S*Vol*norm.pdf(d_uno))/(2*sqrt(T) - r*K*exp( -r*T)*norm.cdf(d_dos)
    Vega = S *sqrt(T)*norm.pdf(d_uno)
    Rho = K*T*exp(-r*T)*norm.cdf(d_dos)
    return Delta, Gamma, Theta, Vega , Rho

En el caso de las opciones de venta:

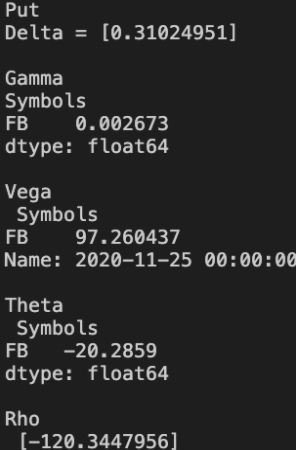
def BSMPutGreeks(S, K, r, Vol, T):
    d_uno = d1(S, K, r, Vol, T)
    d_dos = d2(S, K, r, Vol, T)
    Delta = norm.cdf(-d_uno)
    Gamma = norm.pdf(d1)/(S*Vol*sqrt(T))
    Theta = -(S*Vol*norm.pdf(d_uno)) / (2*sqrt(T))+ r*K * exp(-r*T) * norm.cdf(-d_uno)
    Vega = S *sqrt(T) * norm.pdf(d_uno)
    Rho = -K*T*exp(-r*T) * norm.cdf(-d_dos)
    return Delta, Gamma, Theta, Vega, Rho

Para añadir un dividendo contínuo, sólo habría que añadir un parámetro "d": BSM(S, K, r, Vol, T, d) y modificar las fórmulas.