Cálculo de métricas y retornos

En este artículo vamos a ejemplificar una serie de cálculos sencillos pero útiles a la hora de determinar el desempeño de un activo o cartera de inversión. Para el ejemplo voy a utilizar los tickers de las siguientes empresas: Microsoft, Union Pacific, Google e IBM.

Procedemos a la descarga del precio ajustado de los precios de cierre a partir de 2019 hasta fecha de hoy.

import numpy as np
from pandas_datareader import data as wb

assets = ['MSFT','UNP','GOOG','IBM']
data = wb.DataReader(assets,'yahoo','2019-1-1')['Adj Close']

A continuación calculamos los retornos simples y logarítmicos. Los simples consisten en la variación entre el precio de cierre de hoy con el de ayer, en tanto por uno, se realizan con la función pct_change()

returns = data.pct_change()[1:]
log_returns = np.log(1 + data.pct_change()[1:])

Los retornos logarítmicos difieren de los simples en que facilitan la suma de rendimientos en el tiempo. Pasar de 100€ a 105€ nos daría una subida de 4,879%, exactamente la misma que de bajada, retornos sumados que darían 0. 

Si asumimos cierta normalidad en los retornos y pensamos que un activo tiene la misma probabilidad de subir o bajar, deberíamos considerar la utilización de los retornos logarítmicos.

Cuanto más bajos sean estos retornos, más se parecen a los obtenidos por rentabilidad simple, esto nos viene bien para analizar múltiples pequeñas operaciones de c/p.

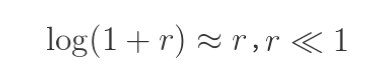
Esta diferencia se acrecienta cuanto más dispares son los valores usados para el cálculo. Por lo que para grandes retornos no es tan aconsejable, ni tampoco para analizar comparativamente muchos valores.

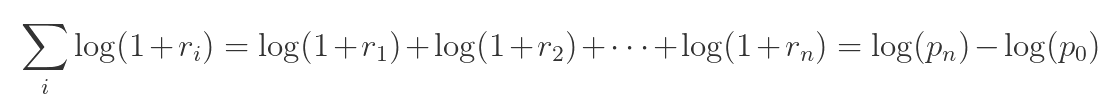
El rendimiento compuesto durante n periodos es simplemente la diferencia en logaritmo entre los precios inicial y final. (Para el ejemplo seguiremos con los cálculos a partir de los simples.)

Una vez disponemos de los retornos, podemos calcular el retorno acumulado (normalización del precio), se puede entender como cuánto crece el valor en usd a través del tiempo partiendo de un mismo momento. Podemos utilizar la función cumprod() y pasarle fillna(1), así comprobaremos la evolución partiendo de 1 usd, por ejemplo.

returns = data.pct_change()

cummulative_r = (1+returns).cumprod()
cummulative_r.fillna(1, inplace = True)

Podemos graficarlo:

import matplotlib.pyplot as plt
cummulative_r.plot()
plt.show()

Es exactamente el mismo proceso que si dividimos cada activo por su precio inicial, como hacíamos anteriormente con gráficos en escala relativa.

data = data/data.iloc[0]

Para anualizar los retornos, podemos utilizar .shape para conocer el tamaño de nuestro DataFrame (días bursátiles) o podemos usar len(), luego debemos elevar los retornos al año bursátil dividido entre el total de periodos.

annualized_cummulative = cummulative_r[1:]**(252/len(cummulative_r))-1

También podemos calcular estadística descriptiva y medidas de dispersión con respecto a la media para un periodo de tiempo de forma fácil y sencilla: la media .mean(), desviación estándar .std(), varianza .var(), covarianza .cov() , el coeficiente de correlación .corr(), la mediana .median()...

returns.mean()
returns.var()
returns.cov()
returns.corr()
returns.std()

Podemos también realizar una media móvil (simple) y desviación estándar para periodos específicos que recorran toda la muestra de datos con la función rolling() y graficarlas. Para una exponencial podríamos usar el método ewm() de pandas.

period = 30
MAvrg = data.rolling(period).mean().iloc[period:]
Mstd = returns.rolling(period).std().iloc[period:]

Podemos graficar ambas:

plt.plot(data.index,data,MAvrg)
Mstd.plot()
plt.show()

Para acabar, podemos calcular el Drawdown de activos de forma individual de la siguiente manera:

peaks = cummulative_r.cummax()
dd = (cummulative_r - peaks)/peaks
mdd = dd.min()

Se necesita calcular los máximos relativos del activo, luego el drawdown y con .min() obtendríamos la caída máxima absoluta para el periodo.

Algo que todavía no hemos visto aún es la anualización de la volatilidad, que no deja de ser la desviación estándar de los retornos (si asumimos normalidad en su distribución) multiplicada por la raíz cuadrada del tiempo, en este caso 252 días. Para poder hacer el cálculo de la desviación, primero debemos tener todos los datos de rentabilidad en una misma medida temporal. La volatilidad no se incrementa en la misma proporción que la rentabilidad sino que crece como la raíz cuadrada del tiempo. 

returns.std()
Vol_annual = returns.std() * np.sqrt(252)

En cambio para hacer diario un dato de volatilidad anual deberíamos dividirlo.

Podemos también calcular el ratio Sharpe utilizando la fórmula:

Necesitamos descargarnos el último valor de la tasa libre de riesgo a 10 años de EE.UU, en tanto por uno, el ticker corresponde a: ^TNX

rf = data['^TNX'][-1]/100

A continuación podemos crear un DataFrame para tener los datos en columnas y aplicar la fórmula:

df = pd.DataFrame(index=returns.columns)
df['CAGR'] = annualized_cummulative.iloc[-1].round(3)
df['Vol_annual'] = Vol_annual.round(3)
df['Sharpe'] = ((df['CAGR'] - rf)/ df['Vol_annual'])

Podemos trabajar con una cartera en lugar de acciones individuales, si construímos un array con los pesos para cada activo:

weights = ([0.25,0.25,0.25,0.25])

En este caso sería una cartera donde cada activo ocuparía el 25% de la inversión.

Calcularíamos los retornos anualizados o CAGR de la cartera:

cartera_cagr = np.dot(annualized_cummulative.iloc[-1],weights)

También podemos calcular los retornos ponderados para esta cartera, equilibrada al 25%:

returns['Portfolio weighted'] = returns.dot(weights)

Al igual que también su Drawdown:

peaks_portfolio = returns.dot(weights).cummax()
dd_portfolio = ((returns.dot(weights) - peaks_portfolio) / peaks_portfolio)
ddp_min = dd_portfolio.min()
dd_portfolio.plot()
plt.show()

Algo que hemos utilizado en el modelo del VaR de forma indirecta es el cálculo de la volatilidad para una cartera:

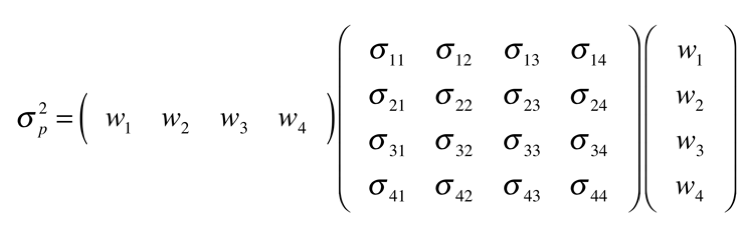
La variación en una cartera consta de las multiplicaciones de la matriz de los pesos transpuesta (1x4), la matriz de covarianzas y la matriz de los pesos sin transponer (4x1) (Siendo 4 en este caso debido al número de activos en nuestra cartera para el ejemplo.)

cov = returns.cov()*252
port_var = np.sqrt(np.dot(weights.T, np.dot(cov, weights))).round(3)