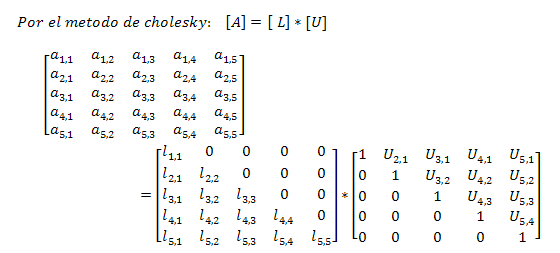El método de Monte Carlo

Gerard Sánchez - 11 de Diciembre de 2020 a las 21:31 - Modelos

“We do not need to be rational and scientific when it comes to the details of our daily life — only in those that can harm us and threaten our survival. Modern life seems to invite us to do the exact opposite; become extremely realistic and intellectual when it comes to such matters as religion and personal behavior, yet as irrational as possible when it comes to matters ruled by randomness.” (Fooled by Randomness).

"Lo que llamamos azar es nuestra ignorancia de la compleja maquinaria de la causalidad". (Jorge Luis Borges)

¿Existe el azar o en realidad todos los fenómenos del universo son parte de una cadena de causalidades?

El azar influye de forma acuciante en el comportamiento de los mercados, la bolsa, y las inversiones, casi cualquier hecho o comportamiento se puede modelar y tratar en base a una suma de factores conocidos y desconocidos -empleando, por ejemplo, métodos como el de Monte Carlo-.

Este método trata de generar escenarios reales de forma aleatoria en base a una distribución subyacente previamente estipulada, y de esta forma, ser capaz de aproximarnos estadísticamente a un escenario plausible en el futuro. Es una técnica que se utiliza para comprender el impacto del riesgo y la incertidumbre al tomar una decisión.

Las simulaciones de Monte Carlo pueden ser una pieza más de nuestra estrategia de análisis a la hora de valorar una acción u operación.

El punto de partida es disponer de los precios de cierre, los que conocemos, queriendo predecir los precios a futuro, junto a su % de variación o tasa de retorno r. Los precios se ajustan a una distribución log-normal con una media conocida y una desviación estándar multiplicada por un componente aleatorio.

Con lo cual tenemos que:

Cómo calculamos el rendimiento?

El movimiento Browniando es un proceso estocástico utilizado para modelar el comportamiento aleatorio a lo largo del tiempo. Se utiliza mucho en los campos de la física, química, estadística o finanzas. Para simplificar, usaremos el movimiento browniano simple o artimético (ABM), en lugar del movimiento browniano geométrico (GBM), que es más adecuado cuando trabajamos con acciones.

El método Browniano consta de 2 partes; el Drift y la volatilidad:

El Drift consiste en un factor de ajuste o tasa de crecimiento, es la dirección que han tenido las tasas de rendimiento en el pasado, si es positiva la tendencia aumentará y bajará en caso de ser negativa.

Calcularemos la volatilidad, en este caso, como la desviación estándar de los retornos logarítmicos por una variable aleatoria normal que más adelante definimos.

Finalmente, la fórmula desarrollada nos queda así:

Para empezar, descargamos los datos del periodo y la empresa que nos interese, siendo 'AMZN' en este caso.

Para esto, es mejor si definimos una función que importe datos diarios de acciones para cualquier empresa que cotice en bolsa a partir de una fecha definida por el usuario hasta hoy, usando los precios de cierre ajustados como venimos haciendo normalmente.

ticker = 'AMZN'
data = pd.DataFrame()
data[ticker] = wb.DataReader(ticker, data_source='yahoo', start='2018-1-1')['Adj Close']

Calculamos los retornos logarítmicos junto a su media, la varianza , la volatilidad, y el factor de ajuste.

log_returns = np.log(1+data.pct_change())
u = log_returns.mean()
var = log_returns.var()
drift = u - (0.5*var)
stdev = log_returns.std()

Con las variables days y trials definiremos el periodo a futuro para el cual ejecutaremos las pruebas, así como el número de ellas.

Los cálculos pueden hacer aumentar considerablemente el tiempo de computación necesario para procesar los resultados, así que ten cuidado, no vaya a ser que se te bloquee el ordenador, piensa que se multiplica cada día por el número de pruebas.

days = 100
trials = 10000

Calculamos con el método norm.ppf que ya hemos visto en anteriores entregas (one tail test) y generamos valores al azar para una matriz definida: days,(filas), trials,(columnas).

Z = norm.ppf(np.random.rand(days, trials))

Ahora generamos los rendimientos diarios (que no precios) para cada día en el futuro para cada iteración (simulación) basada en una distribución normal.

Para dibujar las líneas móviles para cada uno de los días, y que muestran el clásico gráfico de simulaciones, tenemos que construir una matriz del mismo tamaño que nos servirá luego para hacer las multiplicaciones y con iloc[-1] dejamos fijamos nuestro día 0 para el cálculo (S_t-1).

retornos_diarios = np.exp(drift.values + stdev.values * Z)
camino_de_precios = np.zeros_like(retornos_diarios)
camino_de_precios[0] = data.iloc[-1]

Hacemos un bucle para el número de días de nuestra elección con la variable days y hacemos la multiplicación de la matriz generada anteriormente. con los retornos_diarios:

for t in range(1, days):
    camino_de_precios[t] = camino_de_precios[t-1]*retornos_diarios[t]

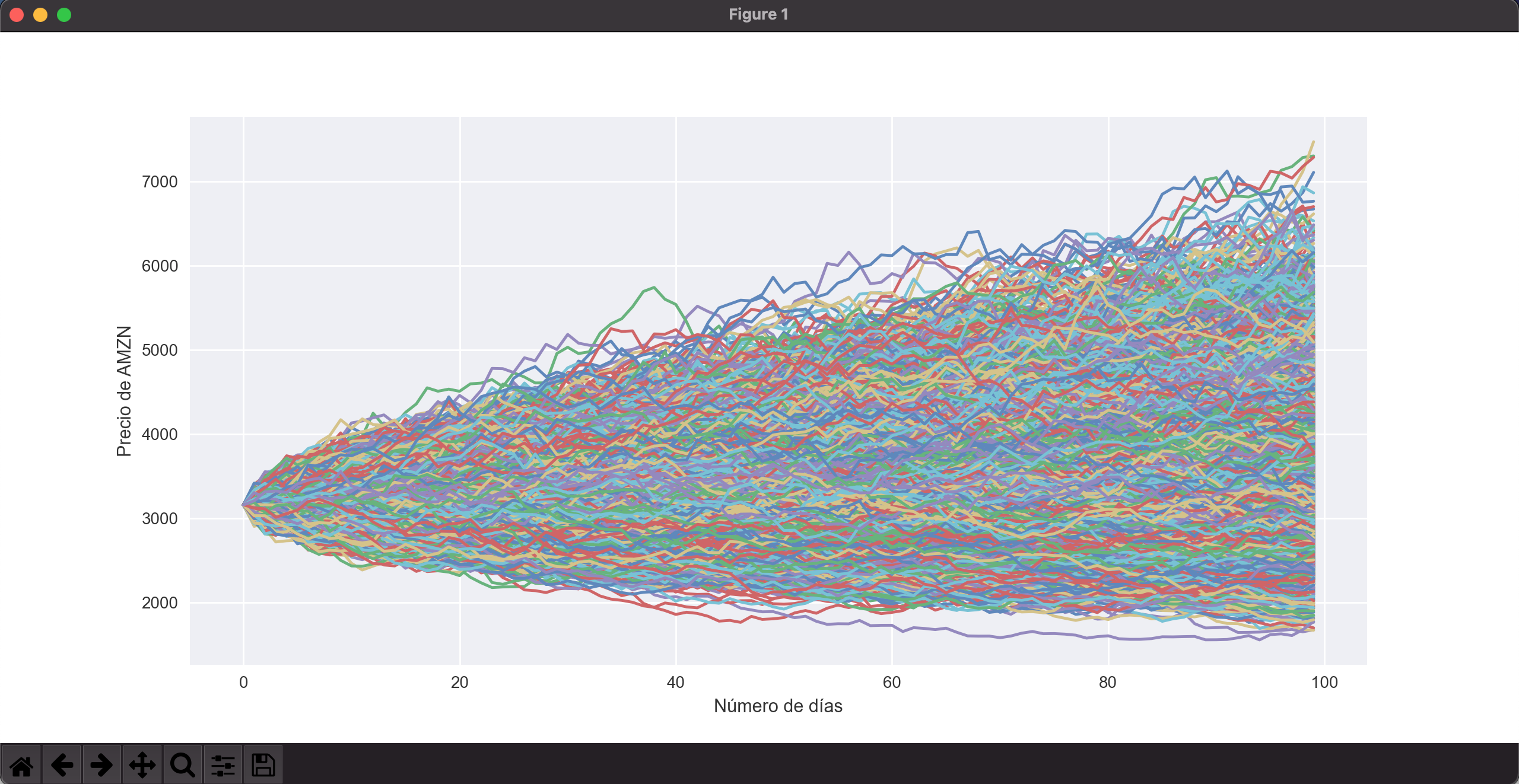
Con matplotlib y seaborn graficamos los resultados del primer gráfico en (15,6) de resolución (para facilitar su visionado), generando simulaciones de líneas para unir cada uno de los días con su respectiva evolución y un histograma del día final de precios finales para cada simulación.

plt.figure(figsize=(15,6))
plt.plot(pd.DataFrame(camino_de_precios))
plt.xlabel("Número de días")
plt.ylabel("Precio de " + ticker)
sns.displot(pd.DataFrame(camino_de_precios).iloc[-1])
plt.xlabel("Precio a " + str(days) + " días")
plt.ylabel("Frecuencia")
plt.show()

El resultado de la simulación es claro. A 100 días vista con 10.000 iteraciones, comprobamos cómo los precios con mayor frecuencia se encuentran en la franja de los 3100-3500, con cierta asimetría positiva (skewness derecho), teniendo un precio S_t-1 de 3162$.

Aquí tienes el script entero:

import numpy as np
import pandas as pd
from pandas_datareader import data as wb
import matplotlib.pyplot as plt
from scipy.stats import norm
import seaborn as sns
from matplotlib import style

style.use('seaborn')

ticker = 'AMZN'
data = wb.DataReader(ticker, data_source='yahoo', start='2018-1-1')['Adj Close']

log_returns = np.log(1+data.pct_change())

u = log_returns.mean()
var = log_returns.var()
drift = u - (0.5*var)
stdev = log_returns.std()
days = 100
trials = 10000

Z = norm.ppf(np.random.rand(days, trials))
retornos_diarios = np.exp(drift.values + stdev.values * Z)
camino_de_precios = np.zeros_like(retornos_diarios)
camino_de_precios[0] = data.iloc[-1]

for t in range(1, days):
    camino_de_precios[t] = camino_de_precios[t-1]*retornos_diarios[t]

plt.figure(figsize=(15,6))
plt.plot(pd.DataFrame(camino_de_precios))
plt.xlabel("Número de días")
plt.ylabel("Precio de " + ticker)
sns.displot(pd.DataFrame(camino_de_precios).iloc[-1])
plt.xlabel("Precio a " + str(days) + " días")
plt.ylabel("Frecuencia")
plt.show()

He realizado otra prueba de concepto de las Simulaciones de Montecarlo, en este caso para un portafolio

En este caso para una cartera con unos activos y pesos determinados, siguiendo la factorización de Cholesky para darle estabilidad numérica y simular sistemas con variables múltiples correlacionadas.

El proceso consiste en descomponer esta matriz de correlación entre los activos para obtener la triangular inferior "L", para a continuación multiplicar esta por un vector de ruidos simulados "u" descorrelacionados. Con esto obtendremos un vector "Lu" que mantiene las propiedades de covarianza del sistema a ser modelado.

Imagen

L = np.linalg.cholesky(covar)
u = norm.ppf(np.random.rand(num_stocks, num_stocks))
Lu = L.dot(u)

Y aquí el código:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pandas_datareader import data as wb
from scipy.stats import norm
import seaborn as sns

tickers = ['FB', 'AAPL', 'MSFT', 'IBM', 'TSLA']
num_stocks = len(tickers)

weights = np.random.random(num_stocks)
weights /= np.sum(weights)

# Cartera Modelo 
# weights = [0.x, 0.y, 0.z...]

data = wb.DataReader(tickers, 'yahoo', '2015-1-1')['Adj Close']
logr = np.log(1+data.pct_change()[1:])

m = logr.mean()
var = logr.var()
drift = m -(0.5*var)
covar = logr.cov()
stdev = logr.std()

trials = 100
days = 1000

Simulaciones = np.full(shape=(days, trials), fill_value=0.0)

Cartera = float(500000)

L = np.linalg.cholesky(covar)
u = norm.ppf(np.random.rand(num_stocks, num_stocks))
Lu = L.dot(u)

for i in range(0, trials):
    Z = norm.ppf(np.random.rand(days, num_stocks))
    retornos_diarios = np.inner(L, drift.values + stdev.values*Z)
    Simulaciones[:,i] = np.cumprod(np.inner(weights, retornos_diarios.T)+1)*Cartera
    Simulaciones[0] = Cartera

plt.figure(figsize=(15,8))
plt.plot(Simulaciones)
plt.ylabel('Valor de la cartera')
plt.xlabel('Días')
plt.title(' Simulación de Montecarlo para ' + str(Cartera) + "€\n" + str(tickers) + "\n" + str(np.round(weights*100,2)))
sns.displot(pd.DataFrame(Simulaciones).iloc[-1])
plt.ylabel('Frecuencia')
plt.xlabel('Cartera')
plt.show()