El modelo CAPM en Python

En toda inversión está presente el binomio inamovible entre rentabilidad y riesgo, una relación directa que define absolutamente el comportamiento del ser humano en su forma de interactuar con la naturaleza, por la cual numerosos economistas han basado sus estudios a la hora de desarrollar modelos, como por ejemplo Sharpe. El objetivo se basaba en encontrar el punto óptimo en una cartera entre un retorno esperado lo más alto posible, en contraposición con un riesgo mínimo

Entre 1964 y 1966 William Sharpe, en colaboración con otros, desarrolla el modelo CAPM (Capital Asset Pricing Model), una teoría conjunta sobre la formación de precios en activos financieros. Sirve de base de estudio para economistas y científicos que intentan o pretenden mejorarlo para elaborar el modelo que mejor se adapte a la realidad económica. Acabará siendo pieza fundamental dentro de la teória moderna de gestión de carteras (MPT), desarrollada por Markowitz en los 50.

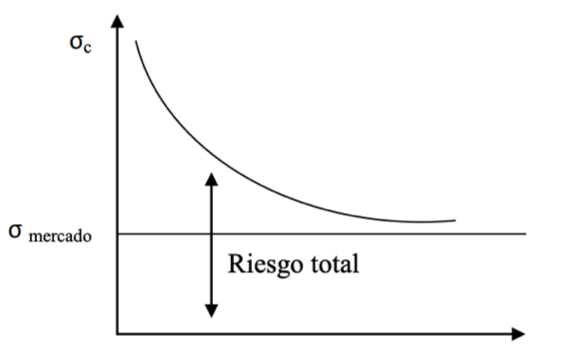
William Sharpe concibió una forma de entender el riesgo; existía una parte sistemática que venía dada por fluctuaciones del mercado, es decir, por las variables macroeconómicas, y que es inherente al mercado, siendo este incapaz de eliminarse por completo. La otra parte consiste en el riesgo específico del activo en cuestión, minimizable con la incorporación de un mayor número de activos a la cartera, o sea, diversificando.

La rentabilidad esperada de un activo viene determinada por:

La tasa "libre de riesgo", la prima del riesgo de mercado o rentabilidad adicional por asumir riesgo y la volatilidad del valor con respecto a las variaciones del mercado.

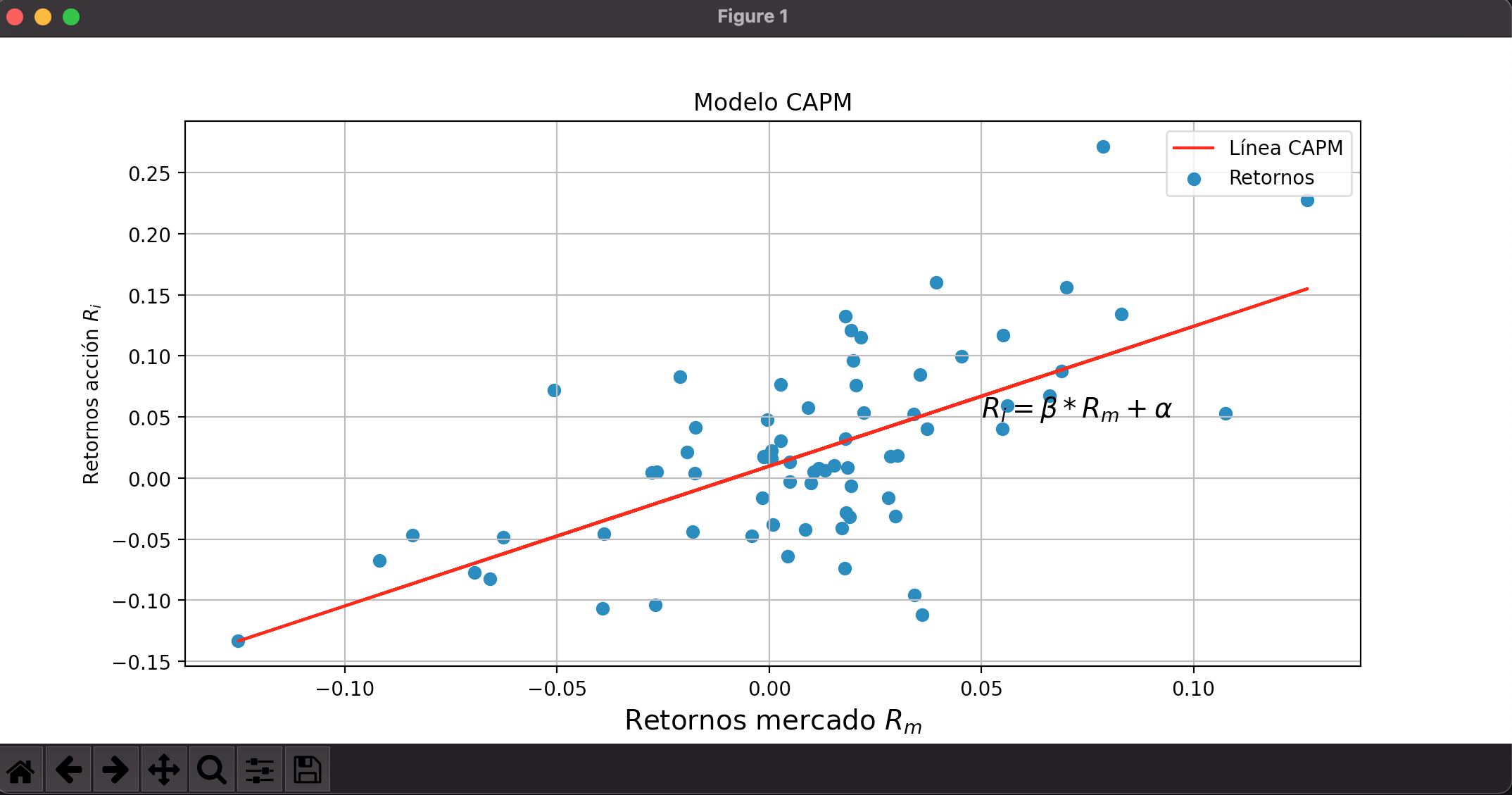
La beta se puede calcular a través de una regresión entre la rentabilidad del activo y del mercado. 

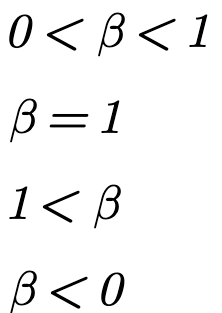
Si la beta se encuentra entre cero y uno, se trataría de un activo defensivo ya que es menos arriesgado que el mercado. Cuando el mercado sube, el activo lo hace con menor intensidad, y viceversa.

Para la cartera de mercado, la beta es igual uno, moviéndose a la par que el índice o benchmark.

En el caso de tener títulos agresivos con beta superior a uno significa que el activo o cartera se mueve en mayor proporción que el benchmark, tanto al alza como a la baja.

Que la beta sea igual a cero quiere decir que la covarianza del activo con respecto al mercado es cero. Esto ocurriría con el activo libre de riesgo, por ejemplo. 

Por último, una beta menor que cero, es decir, que su covarianza es negativa, se refiere a los títulos cuya correlación con el mercado es inversa. Se trata de activos refugio como por ejemplo el Oro.

Vayamos a la parte más técnica, de la mano de Python.

Para el ejemplo en cuestión automatizaremos los cálculos relativos al modelo para un activo del mercado USA, donde es más fácil establecer una tasa libre de riesgo adecuada y el volumen de negociación es más alto con lo que los retornos se determinan con más capital negociado.

Como siempre primero hacemos el bucle para descargar los datos para el periodo escogido (el que creáis conveniente), en este caso utilizaremos $TSLA y el benchmark sp500 $^GSPC.

tickers = ['TSLA','^GSPC']

data = pd.DataFrame()
for t in tickers:
    data[t] = wb.DataReader(t, data_source='yahoo', start='2017-1-1')['Adj Close']

 Calculamos los retornos logarítmicos y sacamos la covarianza anualizada entre los dos.

log_returns = np.log(1 + data.pct_change())
cov = log_returns.cov()*252

Fijamos el dato 0,055227 con iloc[0,1], sacamos la varianza .var() anualizada del SP500 y con esto tendremos las Betas.

cov_with_market = cov.iloc[0,1]
market_var = log_returns['^GSPC'].var()*252
stock_beta = cov_with_market / market_var

Definimos un riskfree, siendo este el rendimiento del bono a 10 años estadounidense, a precio de cierre de ayer de 0,95%, lo ponemos en tanto por uno y nos acordamos de cambiar la coma por un punto, cosas de Python.

Para el riskpremium calculamos la fórmula: 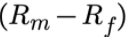anualizando la media de los retornos del SP500 menos el riskfree.

riskfree = 0.0095
riskpremium = (log_returns['^GSPC'].mean()*252) - riskfree

Generamos la variable de la fórmula del CAPM, stock_capm_return, y otra para el ratio Sharpe, que mide el grado de rentabilidad ajustado por el riesgo, cuanto mayor sea éste mejor.

stock_capm_return = riskfree + stock_beta * riskpremium
sharpe_stock = (stock_capm_return - riskfree) /(log_returns['TSLA'].std()*252**0.5)

La Cartera de Mercado (M) es aquella cartera que, dentro de la frontera de inversiones eficientes, tiene mayor pendiente o Ratio de Sharpe.

Y con print sacamos los 3 resultados que buscamos: Beta, CAPM y Sharpe.

Aquí te dejo el script entero:

import numpy as np
import pandas as pd
from pandas_datareader import data as wb

tickers = ['TSLA','^GSPC']

data = pd.DataFrame()
for t in tickers:
    data[t] = wb.DataReader(t, data_source='yahoo', start='2017-1-1')['Adj Close']

log_returns = np.log(1 + data.pct_change())
cov = log_returns.cov()*252

cov_with_market = cov.iloc[0,1]
market_var = log_returns['^GSPC'].var()*252
stock_beta = cov_with_market / market_var

riskfree = 0.0095
riskpremium = (log_returns['^GSPC'].mean()*252) - riskfree

stock_capm_return = riskfree + stock_beta * riskpremium
sharpe_stock = (stock_capm_return - riskfree) /(log_returns['TSLA'].std()*252**0.5)

print("La Beta de " + str(tickers) + " es de: " + str(round(stock_beta,3)))
print("El retorno CAPM de " + str(tickers) + " es de: " + str(round(stock_capm_return*100,3))+"%")
print("El Ratio Sharpe de " + str(tickers) + " es de: " + str(round(sharpe_stock,3)))

Para el caso de una cartera el proceso es parecido, sólo necesitaríamos realizar el mismo proceso descargando los datos para el resto de activos en la cartera y con una variable con los pesos en forma de matriz con np.array(). La beta de una cartera es la suma ponderada de las individuales.

No hemos hablado de ello pero este modelo tiene limitaciones, como absolutamente todos: Cuestiones sobre la fiabilidad de la beta, mercado eficiente, racionalidad en la toma de decisiones, horizonte temporal de inversión y expectativas sobre los retornos, información disponible para todos... Su facilidad de aplicación hace que sea un modelo útil si lo compaginamos, por supuesto, con otras técnicas y enfoques de valoración, pero no es recomendable dejarse influir demasiado por sus resultados, más allá de la obtención de unos datos estadísticos aproximados.