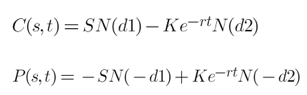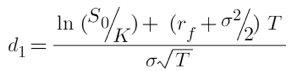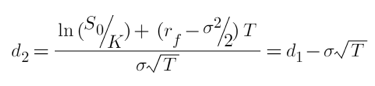Dentro del apasionante mundo de los derivados, y más concretamente el de las opciones financieras, nos encontramos con el problema de poder cuantificarlas. A este problema le intenta dar solución el modelo Black-Scholes, entre otros como el modelo binomial, resolviendo el valor de la prima de una opción en un mercado "libre de riesgo", que poco o nada tiene que ver con el real, pero que ayuda a aproximar un precio bajo ciertas premisas teóricas.

Para entender las griegas es necesario un pequeño repaso y entendimiento del modelo Black-Scholes.

Para que este modelo tenga sentido, parte de las hipótesis siguientes:

-Las variaciones en el precio del subyacente siguen una relación log-normal y son independientes entre sí, (permite subidas de precio ilimitadas y caídas del mismo hasta 0, cosa que la distribución normal no, cuando contamos con infinitos periodos).

-Utilizamos un criterio de volatilidad constante.
-El subyacente no reparte dividendo al menos hasta vencimiento o éste es constante.
-La tasa de interés "libre de riesgo" es constante.
-Sin costes de transacción, comisiones o tasas durante el tiempo de vida de la opción.
-Liquidez y negociación contínua, sin gaps en el precio.

La fórmula es la siguiente: 

Con estas dos fórmulas se encuentra el valor de la prima de una opción Call o Put para un subyacente () y tiempo hasta vencimiento () determinados.

En Black-Scholes,  es la probabilidad de que la opción de compra (Call) sea ejercida y que por tanto el subyacente sea mayor al strike.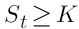 

 Representa la ponderación de la probabilidad de la opcíon de compra siendo ejercida, por el valor del subyacente para un momento determinado.

La probabilidad de que la opción no sea ejercida, multiplicado por el descuento contínuo de la tasa libre de riesgo durante el tiempo de vida que le quede a la opción por su precio de ejercicio, viene determinado por . Se puede entender como lo que pagamos por la opción, expresa el coste de oportunidad de pagar el valor temporal o premium frente a la "tasa libre de riesgo".

 Es la desviación estándar de los retornos logarítmicos. Se asume constante.

La Volatilidad implícita asume el modelo, pero con  como parámetro libre, fijando  y , con estos supuestos se puede despejar  obteniendo para ésta una fórmula que depende de los otros parámetros del modelo (esto supone que la volatilidad está ”incluida” en el precio). Se puede despejar en la fórmula obteniendo el valor de las primas a precio de mercado. 

Aquí te muestro un ejemplo numérico resuelto con este modelo.

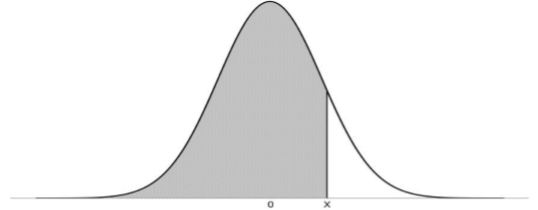
Entendemos N(x) como la función de probabilidad acumulada N. Es la probabilidad de que una variable sea menor o igual a x. Aquí te dejo la tabla de probabilidades para N(d).

El área sombreada representa la posibilidad de que a vencimiento, 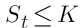 y el comprador no ejerza la opción (OTM): .

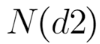Ahora podemos entender las griegas.

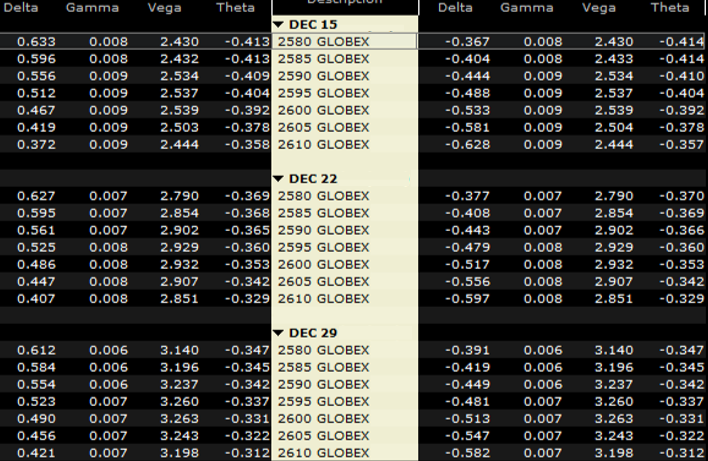
Existen 5 principales variables, denominadas “Las Griegas”, en referencia a la utilización del alfabeto griego para denominarlas. Delta (δ ), Gamma (γ Γ), Theta (θ Θ), Rho (ρ Ρ) y Vega, la cual no es letra griega pero es la que se usa para referirse a la Volatilidad implícita. Son medidas de sensibilidad para aproximar las primas.

DELTA: 

 Delta mide la variación que existe en la prima ante la variación del precio del subyacente. Por cada usd o pb (unidad) que varíe el activo subyacente la prima variará un porcentaje de esa fluctuación. 

El rango de movimiento de la delta puede oscilar entre (0 y 1) o (-0 y -1). Compra de Call y Venta de Put tienen delta positiva; exposición alcista al mercado, al contrario que la Venta de call y la Compra de Put.

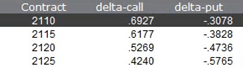
Con una delta de 0,6927 como en el ejemplo, por cada 10 puntos que se moviera el subyacente, nuestra prima subiría 6,927 puntos, ceteris paribus.

Matemáticamente,  se puede expresar como la derivada de la función V del valor o activo con respecto al precio  del subyacente. Este cálculo es útil para ejemplificar de forma teórica y aproximada, además es útil para ver la probabilidad de que esa opción acabe en el dinero. Para un cálculo preciso se requiere Black-Scholes.

Escogiendo un periodo, podemos calcular  en base a las diferencias de la prima y del subyacente entre ese mismo periodo de observación.

Tomando un ejemplo con unas opciones Call, cuya diferencia de valor entre el periodo resultó ser 0,16 y de 2,17 para el subyacente, nuestra seria de 0,073733 aproximadamente. (7.3% de acabar ATM/ITM)

Según el model Black-Scholes,  corresponde a la distribución normal de la función d1 expresada anteriormente:

Donde  y  corresponden a los precios del subyacente y prima respectivamente,  al retorno libre de riesgo (concepto teórico), y  para el valor de la volatilidad (variación realtiva con respecto a su media),  representa el periodo de observación y  la probabilidad de que la opción expire dentro o en el dinero.

La delta de la Call y de la Put siempre suman 1 en valor absoluto, (1-Delta), y tiene propiedades additivas. Podemos calcular cuantas deltas tiene una cartera o portafolio, a fin de poder hacer coberturas delta neutral, para estar expuesto al resto de variables pero no a la variación del subyacente.

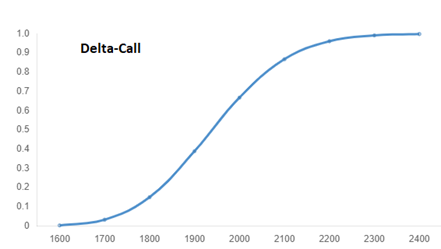
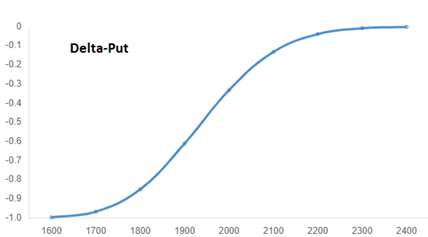
Podemos graficar delta en relación al precio del subyacente, (no al strike del contrato), aquí vemos cómo los mayores incrementos en Delta se producen ATM y ITM, esta curva será más pronunciada o vertical cuanto menor sea el tiempo que nos quede a vencimiento. Un comprador de opciones capitalizará movimientos más grandes ATM o cerca de él. Un vendedor OTM no tendrá grandes cambios excepto ocasiones excepcionales.

Compra de Call:

Compra de Put:

Venta de Call:

Venta de Put:

De forma prática, el valor Delta aproxima la posibilidad de que el subyacente acabe en ese strike o ITM. Por lo tanto, una delta de 0,7 puede aproximar que el mercado cotiza que existen un 70% de posibilidades que esa opción acabe ATM/ITM. Se infiere una relación inversa entre riesgo y Delta. A mayor Delta, menor riesgo y mayor probabilidad de acabar ITM y viceversa.

GAMMA: 

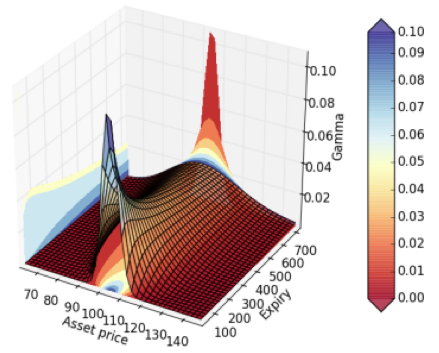
La siguiente griega que nos encontramos es “Gamma” o factor riesgo, refleja el cambio en delta por cada variación unitaria del activo subyacente.

Es la segunda derivada del precio del subyacente y por consiguiente la derivada de delta, y al contrario de la misma, esta tiene el mismo valor tanto para la Call como para la Put para el mismo strike y vencimiento.

Gamma mide la variación de  respecto a variaciones de .

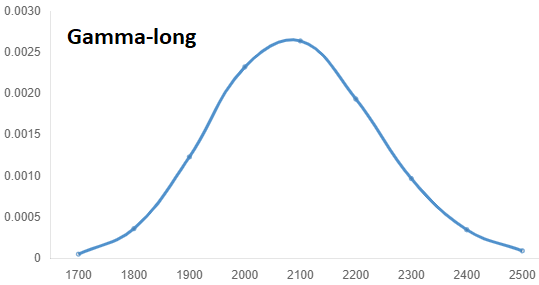
Compras de opciones:

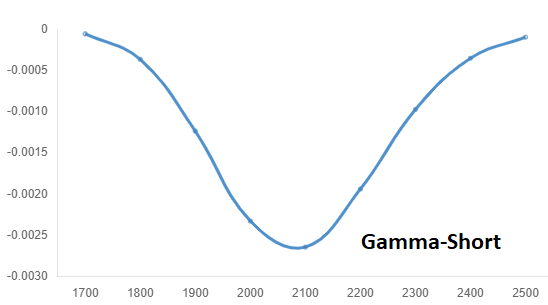
Ventas de opciones:

Al igual que con Delta, Gamma adquiere su valor máximo en ATM y disminuye progresivamente cuando se va acercando a OTM y lo mismo para las fechas valor, cuanto más alejados de vencimiento estemos menos curvatura tendrá.

THETA: 

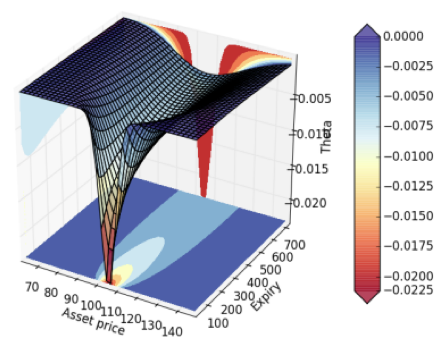
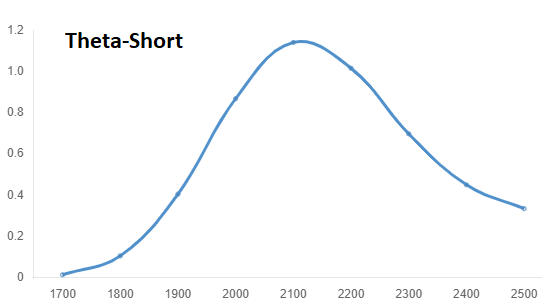
La tercera griega se conoce como Theta o fecha de vencimiento. Tiene una relación directa con el valor temporal, que disminuye con el transcurso del tiempo. Theta mide la variación o sensibilidad de la prima al transcurso del tiempo. Cuánto se reduce el valor teórico de una opción cuando transcurre un día manteniendo volatilidad y precio del subyacente.

Una opción de largo plazo obtiene un valor temporal mayor, ya que estadísticamente tiene más probabilidad de acabar ATM/ITM. Esta posibilidad se reduce cuanto menos tiempo queda a vencimiento.

Esta reducción del tiempo disponible favorece al vendedor de opciones, resultando en una theta positiva (en igualdad de criterios compraremos nuestra opción vendida más barata, con menor valor temporal, de ahí que favorezca) mientras que es negativa para el comprador, pues expresa la pérdida diaria del valor, se conoce vulgarmente como “el sangrado”.

Compras de opciones:

Ventas de opciones:

El segundo término expresa el coste de oportunidad de pagar el valor temporal frente a la tasa libre de riesgo, que se descuenta de forma continua en K durante el periodo a vencimiento.

Theta es la negativa de la derivada de la función del valor de la opción con respecto al tiempo hasta vencimiento.

VEGA: 

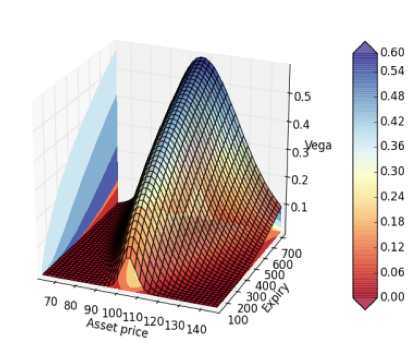
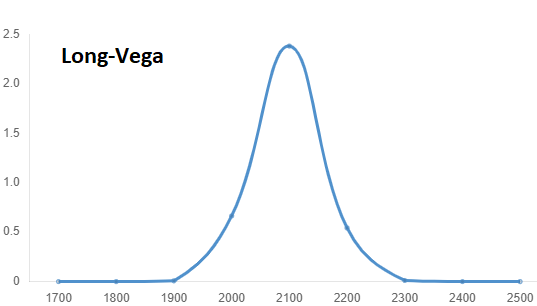
La cuarta variable se conoce como Vega, que mide la sensibilidad a la volatilidad del subyacente, concretamente el cambio en las primas por cada cambio porcentual en la volatilidad, es idéntica tanto en las Calls como en las Puts.

Esta volatilidad se puede calcular a través de la Volatilidad histórica o de la Volatilidad implícita.

La histórica mide el pasado, normalmente se calcula como una desviación estándar de los precios de cierre de un subyacente en los últimos 30 días. Este valor es teórico y sólo sirve de referencia en el mercado, pues se utiliza la Implícita, que engloba expectativas futuras de volatilidad.

La relación directa entre el valor de las primas y la volatilidad se explica por la posibilidad de acabar éstas en el dinero. Mientras más aumente la expectativa de incremento de volatilidad futura, más caras serán estas primas. Las más sensibles las encontramos ATM y ITM cercanas.

El spread entre la volatilidad histórica y la implícita puede hacernos pensar, por reversión a la media, en llevar estrategias contrarias; “short volatility” o “long volatility”, dependiendo de si la implícita es mayor a la histórica o al revés.

Al igual que con las demás griegas, un valor positivo indicará aumento en las primas y un valor negativo, restará.

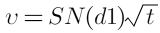
Compras de opciones:

Ventas de opciones:

RHO: 

Rho es la 5ª de las principales griegas que afectan a las primas de las opciones. Mide la sensibilidad en las primas a cambios porcentuales en las tasa de interés libre de riesgo, concretamente el bono estadounidense a 10 años. Es casi un valor teórico ya que el impacto suele ser mínimo, pues los cambios no suelen tener una variación drástica.