Matemática financiera en Python

Las matemáticas financieras, resumidas en una frase, las podríamos definir como la rama de las matemáticas que estudia los flujos de dinero a través del tiempo. Básicamente se presupone que el dinero tiene menos valor en el futuro que en el presente, ya sea por un tema inflacionario o por la preferencia natural de las personas a priorizar el consumo presente.

En este artículo vamos a tratar algunos conceptos básicos (ampliable) de esta rama de las matemáticas, con Python, una herramienta ideal para calcular este tipo de consideraciones.

El VALOR ACTUAL y VALOR FUTURO:

El valor presente de una inversión es cuando calculamos el valor actual que tendrá una determinada cantidad que recibiremos o pagaremos en un futuro. El valor futuro es el valor alcanzado por un determinado capital al final del período determinado (para el ejemplo usaremos la fórmula del interés compuesto).

Sin necesidad de utilizar ninguna librería somos capaces de realizar estos cálculos. Primero creamos 3 variables flotantes para trabajar con una cuota, un tipo de interés determinado y un periodo en el tiempo:

cuota = float()
tipo = float()
periodo = float()

Dentro de una función, introduciremos esas variables como argumentos y crearemos otra condicional a si la cuota está condicionada a ser anticipada o no (1 período más), este input tendrá que introducirlo el usuario al llamar a la función vf() o  va() (1 o 0), aunque a largo plazo el impacto de esta consideración se reduce.

La idea para ambos cálculos, tanto para el valor final como para el actual, es la de calcular de forma recursiva el resultado: res utilizando un bucle for para el número de periodos y empleando la fórmula correcta.

Finalmente redondeamos a 2 decimales el resultado.

def vf(cuota, tipo, periodo,o):
    res=0
    for t in range(periodo):
        if o==1:
            res = res+cuota*(1+tipo)**(t+1)
        else:
            res = res+cuota*(1+tipo)**(t)
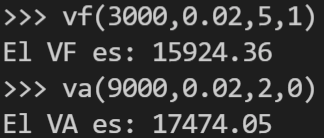
    print("El VF es:", round(res,2))

def va(cuota,tipo,periodo,o):
    res=0
    for t in range(periodo):
        if o==1:
            res=res+cuota/(1+tipo)**(t)
        else:
            res=res+cuota/(1+tipo)**(t+1)
    print("El VA es:", round(res,2))

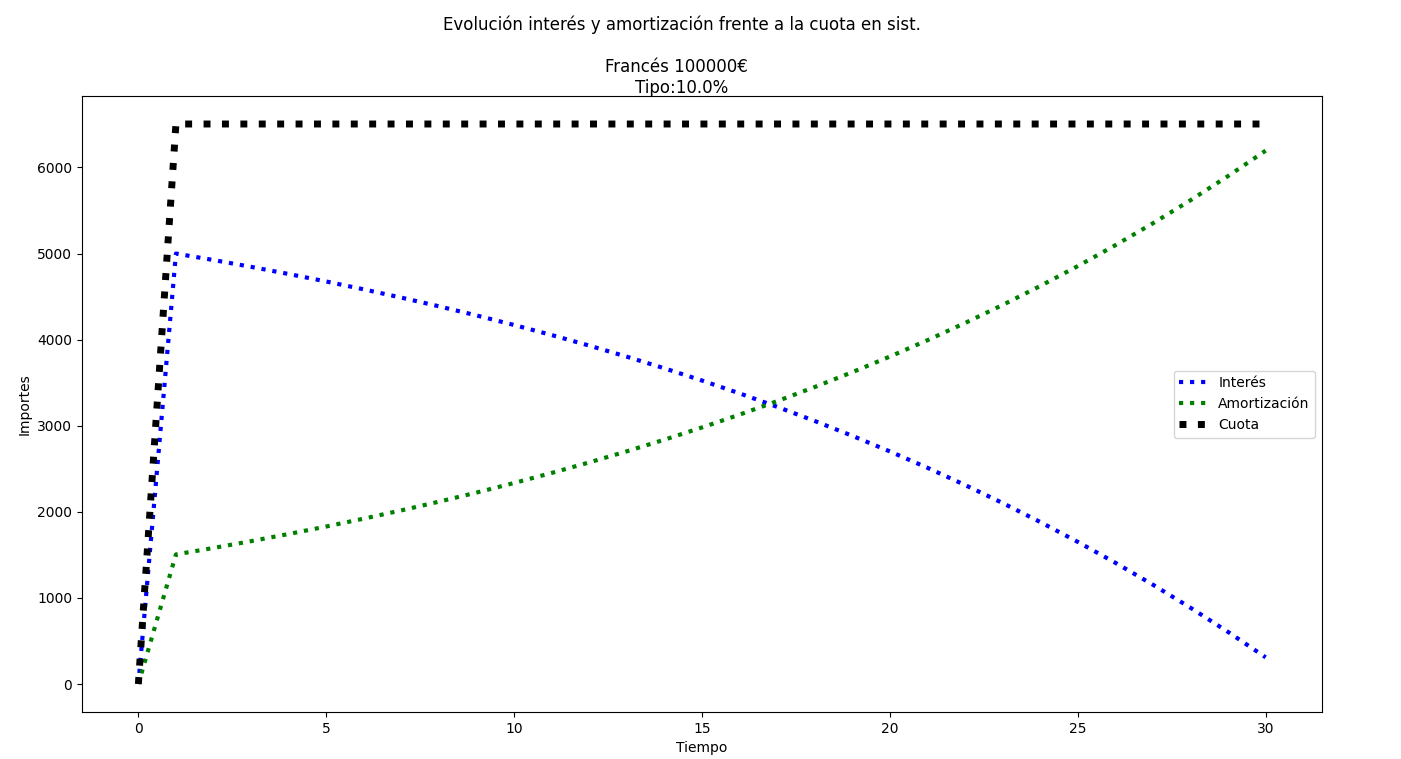
El SISTEMA de AMORTIZACIÓN FRANCÉS:

Se trata de obtener una cuota de amortización constante para un préstamo (generalmente hipotecas para este caso). Se pagan intereses en función del capital pendiente a amortizar, que irá decreciendo a medida que vayamos amortizándolo con nuestra cuota.

Declaramos nuestras variables para proceder a realizar los cálculos y generar nuestro DataFrame. Tenemos una cuota, un capital, un tipo constante, un periodo y un número de pagos al año que podrá modificar nuestro tipo de interés.

import pandas as pd
import matplotlib.pyplot as plt

print('    PRÉSTAMO SISTEMA FRANCES')

cuota = float(0)
capital = int(input('Capital : '))
tipo = float(input('T.int. anual nominal: '))
periodo = int(input('Num. pagos: '))
o = int(input('Pagos por año: '))

Grabamos nuestra fórmula para la cuota y creamos un DataFrame vacío que más adelante rellenaremos a partir de un bucle:

cuota= round(capital*((tipo/(o*100))/(1-(1+(tipo/(o*100)))**(-1*periodo))),2)
print(    'Plan de pagos')

plan = pd.DataFrame(columns=['Cuota','Interes','Amort.','Capital'])
plan.loc[0,'Capital']= capital
plan.loc[0,'Cuota']= 0
plan.loc[0,'Interes']= 0
plan.loc[0,'Amort.']= 0

Con un bucle for para el número total de periodos que el usuario especifique, utilizamos el método loc para ir recorriendo con nuestra variable iterativa todo este DataFrame con la cuota, el cálculo de los intereses en función del capital pendiente, la cuota de amortización y el capital pendiente.

for t in range(1,periodo+1):
    plan.loc[t,'Cuota']= cuota
    plan.loc[t,'Interes']= round(float(plan.loc[t-1,'Capital']*(tipo/(100*o))),2)
    plan.loc[t,'Amort.']= (plan.loc[t,'Cuota']-plan.loc[t,'Interes'])
    plan.loc[t,'Capital']= plan.loc[t-1,'Capital']-plan.loc[t,'Amort.']

print(plan)
print('\nTotal intereses :',round(float(plan['Interes'].sum()),2))

Para finalizar y a modo opcional, dibujamos en un gráfico la evolución de los intereses y la amortización pagada, relación inversa entre ambas.

La TIR no periódica (TIR.NO.PER)

Consiste en la tasa interna de retorno de una inversión en función de una serie especificada de flujos de efectivo que no son necesariamente periódicos. No existe "fórmula" como tal, y hay que hacer un cálculo recursivo delimitando un rango en función del número de decimales de precisión requeridos (2 decimales para nuestro ejemplo)

Una forma de hacer el cálculo para la diferencia entre fechas (cuando el usuario introdujo o extrajo flujos de caja) es transformando cada elemento (AAAA/MM/DD) a días, de forma aproximada, y realizar la diferencia. Una vez hecho esto y pasado a una lista fcha, transformamos cada periodo y lo anualizamos, pasándolo a una lista year.

import numpy as np
import matplotlib.pyplot as plt

print("\n"*2)
print('CÁLCULO DE LA TIR NO PERIÓDICA (MWR)')

cf=[400,200,600,200,-1800]

year=[]
fcha=[]

fecha=['2020/01/01','2020/05/01','2021/01/01','2021/03/01','2021/05/03']

for z in range(len(fecha)):
    fcha.append(int(fecha[z][0:4])*360+int(fecha[z][5:7])*30+int(fecha[z][8:10]))

for z in range(len(fecha)):
    year.append(round(float((fcha[z])-fcha[0])/360,4))

A continuación y para la realización del cálculo, partimos de un bucle while a modo de contador que va a permitirnos hacer ese barrido requerido para una variable i que acabará siendo nuestra TIR.NO.PER.

Necesitamos estimar cuándo nuestro Valor actual neto será 0, y para ello utilizamos una variable vant en la que especificaremos que la condición van>0 sea una columna con "1's" y en caso de que van<0 sea con 0's. La fórmula del van es recursiva y la introducimos dentro de un bucle for para todos los cashflows, variables i, y anualizaciones.

vant=[]
van=float(0)

i=-9999
while i<10000:
    for z in range(len(cf)):
        van = van+(-cf[z]/(1+i/10000)**(year[z]))
    vant.append(np.where(van>0,1,-1))
    van=0 

A continuación, validamos vant y comprobamos que la suma entre estos array 1 y -1 sumados dan 0, lo que implicaría un van=0 y la obtención real de nuestra tasa interna de retorno.

    if len(vant)>1:
        if vant[len(vant)-1]+vant[len(vant)-2]== 0:
            print('el TIR es: ',round(float(i)/100,2),'%')
            tir=round(float(i)/100,2)
    i+=1 # sumamos 0.01% cada paso

A continuación graficamos a modo opcional ese cambio de la variable vant de 1 a -1, en qué momento de i se produce.