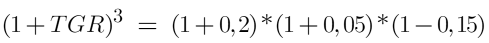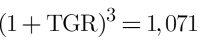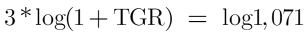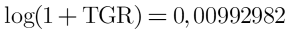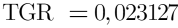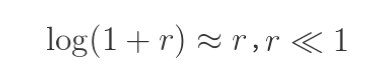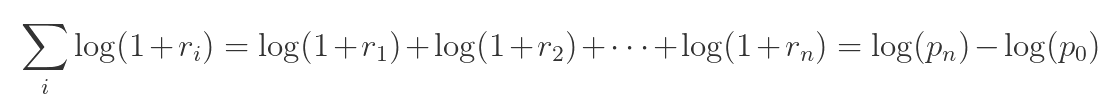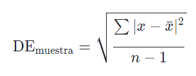Retornos, Riesgo y Volatilidad (Parte I)

Todo el mundo parece estar de acuerdo en que el riesgo es quizá el aspecto de mayor importancia para las personas a la hora de realizar sus inversiones. Siendo esta una de las cuestiones más relevantes dentro del mundo financiero, existen una serie de definiciones subjetivas dependiendo del punto de vista.
Desde un punto de vista financiero, el riesgo significa incertidumbre sobre la evolución de un activo, e indica la posibilidad de que una inversión ofrezca un rendimiento distinto al esperado (tanto a favor como en contra del inversor, aunque lógicamente a éste sólo le preocupa el riesgo de registrar pérdidas)
Este riesgo puede catalogarse de diversas formas dependiendo del escenario en el que nos encontremos. Aquí os dejo un enlace de la CNMV con diferentes tipos de riesgos financieros que existen (aunque hay más).
Por suerte, el riesgo es gestionable. Puede ampliarse, reducirse, cubrirse, diversificarse… pero nunca desaparece del todo. Es sin duda el precio que hay que pagar por el mero hecho de estar expuesto a un precio dinámico en un activo y obtener una rentabilidad, ya sea positiva o negativa.
Existe una correlación positiva entre estas dos variables que casi siempre se cumple (aunque no en la misma proporción) salvo ineficiencias de mercado que rápidamente se arbitran. A mayor riesgo, mayor rentabilidad y a la inversa, aunque no en la misma proporción ni linealidad en el tiempo. Intrínsecamente atado a esto nos encontramos con la aversión al riesgo, que es la actitud de rechazo que experimenta un inversor ante ese riesgo financiero. Una de las mediciones para concretar esa aversión al riesgo de forma matemática es con la medida de volatilidad.
El concepto de volatilidad incluye una serie de factores y consideraciones que hacen de él un tema amplio y complejo. Es sin duda una de las unidades de medida del riesgo por excelencia y de las más utilizadas. La volatilidad expresa la variabilidad de los precios de un activo financiero concreto y se mide generalmente por la desviación estándar de un conjunto particular de rendimientos en un periodo de tiempo determinado. La volatilidad mide por tanto la frecuencia e intensidad de los cambios en el precio de un activo, mostrando la estabilidad o inestabilidad del mismo.
Para entender primero qué es la volatilidad antes necesitamos conocer un poco de estadística. Utilizamos la fórmula de la desviación estándar como medida de dispersión para el cálculo de los retornos:
Primero necesitamos conocer los retornos de nuestra cartera. Para ello podemos usar la rentabilidad aritmética o simple:
Una revalorización de 5€ pasando de p0=100 a p1=105 nos da una rentabilidad simple del 5%, pero si al día siguiente pasamos de 105€ a 100€, la rentabilidad es de -4,76%.
Para calcular retornos continuos en el tiempo hay que hacerlo de forma multiplicativa, por ejemplo, en una inversión de 10000€:
20%+5%
10000+(10000*20%)= 12000
12000+(12000*5%)= 12600…
Muy incómodo.
En rentabilidades simples la relación entre periodos es multiplicativa.
Utilizaríamos la tasa geométrica de rentabilidad (TGR) y no la media aritmética para poder tener en cuenta la relación de capitalización compuesta entre periodos.
Inversión 10000 con rendimientos: (20% + 5% - 15%).
2,313% frente al 3,33% de la media aritmética (incorrecta).
Si asumimos cierta normalidad en los retornos y pensamos que un activo tiene la misma probabilidad de subir o bajar, deberíamos considerar la utilización de los retornos logarítmicos.
Los retornos con la fórmula de la capitalización compuesta continua calculada con logaritmos, nos darían una rentabilidad de 4,879% (en el ejemplo de los 100€ a 105€) tanto de subida como de bajada, retornos opuestos que sumados dan 0. Este cálculo facilita la suma de rendimientos en el tiempo por asumir normalidad en las variables cuando no están correlacionadas, cosa que de forma multiplicativa no se consigue (teoría de la probabilidad).
Cuanto más bajos sean estos retornos, más se parecen a los obtenidos por rentabilidad simple, esto nos viene bien para trading de c/p
Esta diferencia se acrecienta cuanto más dispares son los valores usados para el cálculo. Por lo que para grandes retornos no es tan aconsejable, ni tampoco para analizar comparativamente muchos valores.
El rendimiento compuesto durante n periodos es simplemente la diferencia en logaritmo entre los precios inicial y final.
Ahora que tenemos claro el concepto de rendimientos, podemos hablar de cómo calcular la volatilidad estadísticamente, realizando la raíz cuadrada del sumatorio de la diferencia de los retornos con respecto a su media entre el número de observaciones.
La desviación estándar entendida también como raíz cuadrada de la varianza, mide qué tan dispersos están los datos con respecto a su media. Ya sea la dispersión de los retornos de un activo o las variaciones en la rentabilidad de una cartera.
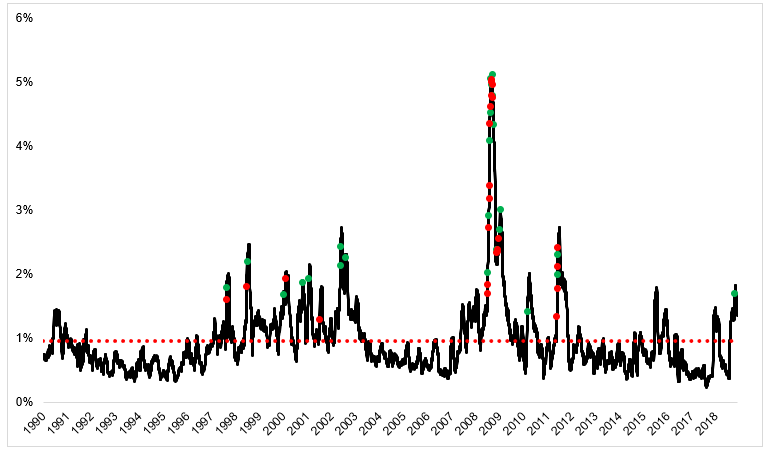
Existen estudios acerca del riesgo y la volatilidad, así como artículos como el vinculado anteriormente, que sin tener en cuenta impuestos, costes de transacciones, etc… realiza una comparativa en base a si te hubieras perdido los mejores y peores 25 días del periodo analizado y un gráfico de largo plazo del “índice del miedo” marcando con puntos verdes los mejores días y en rojo los peores. Los peores días suelen preceder a los mejores, (después de grandes caídas suelen venir grandes rebotes: cierre de cortos + precios baratos + especulación) y los peores suelen estar en periodos de volatilidad por encima de la media, representada por puntos rojos en el primer gráfico.
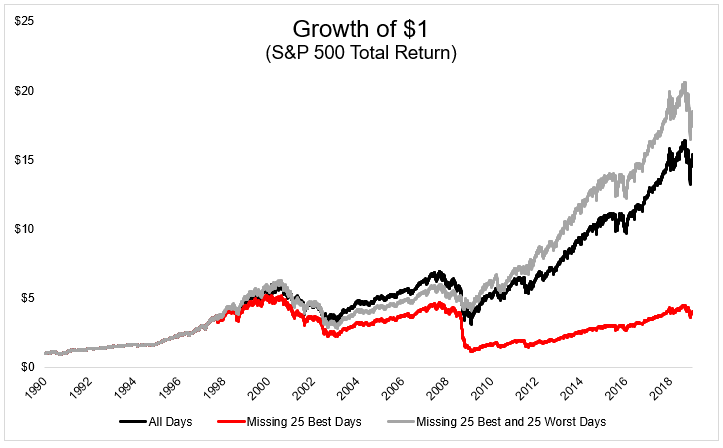
Fuente: Michael Batnick
Comprobamos como la pieza clave son los peores días. Descartando ambos (peores y mejores) nos situaría superando ampliamente al índice, mientras que asumiendo los peores y perdiéndonos los mejores fulminaría nuestra rentabilidad.
1044 visitas
Categorías:
Estrategias Estadísticas Random Gestión pasiva Análisis técnico Modelos CEO Mapas mentales Liberalismo Python Growth Niusleta Ahorro Recursos humanos Inmobiliario Fiscalidad Value investing Dividendos Contabilidad Marketing Riesgo IF Cursos Opciones Bolsa