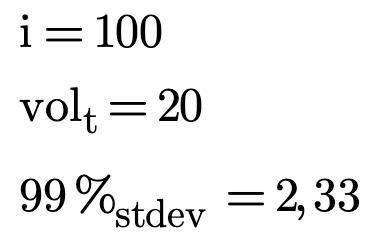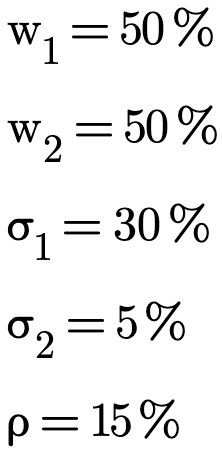VaR como medida de riesgo

Espero no haberte confundido con la imagen de la portada .

La imagen corresponde a otro tipo de VaR, mucho más popular, y no es que no haya también un mercado en el negocio del fútbol (Tebas dixit) y cierto riesgo en la contratación de futbolistas. No, no estamos hablando del “Video assistant referee” en el fútbol u otros deportes, sin embargo ambas comparten relación como herramienta de gestión, en este caso consiste en minimizar el riesgo de cometer un mal arbitraje con sus correspondientes represalias para el árbitro, merma en la reputación y por consiguiente el beneficio o perjuicio para cada uno de los equipos del partido.

En el mundo de los mercados financieros, cualquier evento conocido como cisne negro acaba reflejando la incapacidad de los modelos tradicionales para predecir pérdidas significativas en las carteras de activos financieros. El VaR trata de paliar en parte este asunto.

Para los inversores se trata de gestionar las probabilidades de perder dinero (probabilidades de grandes pérdidas), en ese sentido el VaR se puede utilizar para responder a las preguntas: "¿Cuál es mi peor escenario?" o "¿Cuánto podría perder en un mal día/mes/año...?". 

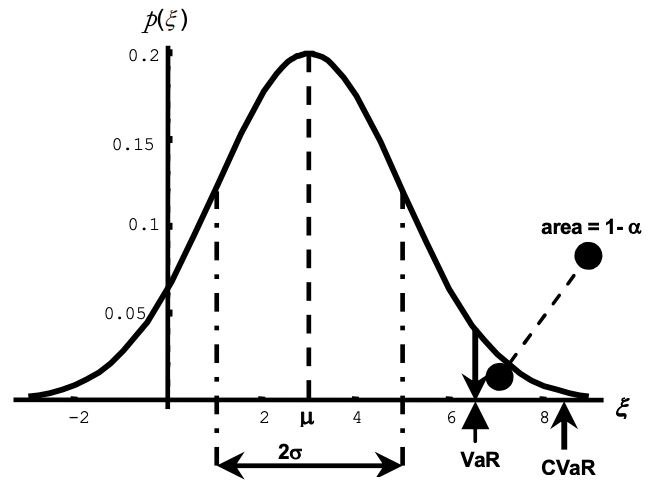
El VaR o Value-At-Risk financiero resume la máxima pérdida para un horizonte objetivo con un nivel de confianza dado. No es sino un determinado percentil de la distribución de probabilidad prevista para las variaciones en el valor de mercado de la cartera en el horizonte de tiempo escogido. Mide el riesgo de mercado, pero no computa riesgos intangibles como el factor humano, operacional, riesgo país, etc... ya que algunos no son del todo cuantitativos.

Al hablar de activos que cotizan en mercados líquidos como son las acciones, puede ser adecuado calcular el VaR a un día o para horizontes temporales muy reducidos, lo cual puede ser reglamentario para traders empleados en mesas de negociación o de tesorería o incluso a nivel particular.

Para las instituciones, el VaR Puede utilizarse como técnica de optimización de carteras si lo usamos activamente para gestionar, ayuda a establecer mínimos de capital requeridos por los bancos según el regulador multiplicando la pérdida máxima por un múltiplo, calidad crediticia, riesgo de insolvencia de algunas entidades, etc... 

Al igual que es capaz de determinar la pérdida máxima gracias a una cola de la distribución, también puede determinar el beneficio máximo potencial de una cartera con los mismos datos con el mismo proceso (VaE, Value at earnings). 

Si tenemos un VaR₍₉₉₎ = 5%, significa que tenemos un 1% de probabilidades de perder un 5% o más para un determinado espacio de tiempo, o lo que es lo mismo, un 99% de posibilidades de perder menos de un 5%. Para el caso de valores únicos, para calcular el VaR solamente necesitaremos su precio de mercado, la media de la desviación estándar de los retornos en un periodo de tiempo (volatilidad) o la implícita y el nivel de significación o confianza. 

Para muestra, el siguiente ejemplo:

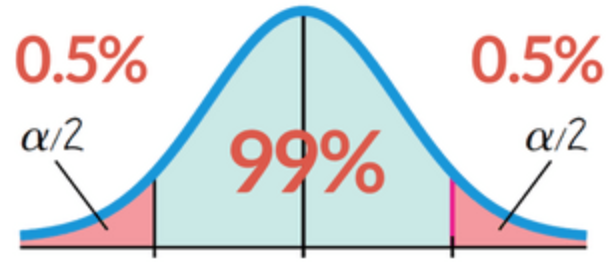
2,33 representan las desviaciones estándar con respecto a la media de una distribución normal con un nivel de confianza del 99%.
(Para los neófitos, un nivel de confianza para una población determinada representa el porcentaje de intervalos que incluirían el parámetro de población escogido.)

Extendiendo el análisis para 2 activos, necesitaremos conocer, a parte de lo anterior para cada uno, el peso realtivo que tienen en cartera y su coeficiente de correlación, que se extrae de la covarianza entre los dos activos. 

En el siguiente ejemplo tenemos el cálculo de la pérdida máxima para un nivel de confianza del 95% a 1 año, siendo 100.000 usd el capital invertido y con los siguientes datos:

El resultado sería que tenemos una pérdida máxima 25.616€, para las especificaciones mencionadas anteriormente.

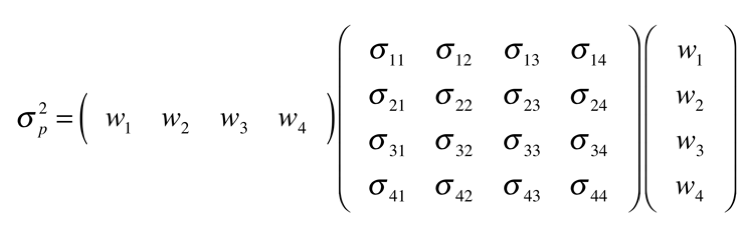
Para más de 3 activos, se necesita generar una matriz para establecer ese coeficiente. Es recomendable trabajar con alguna herramienta, como Python, para automarizar el cálculo.

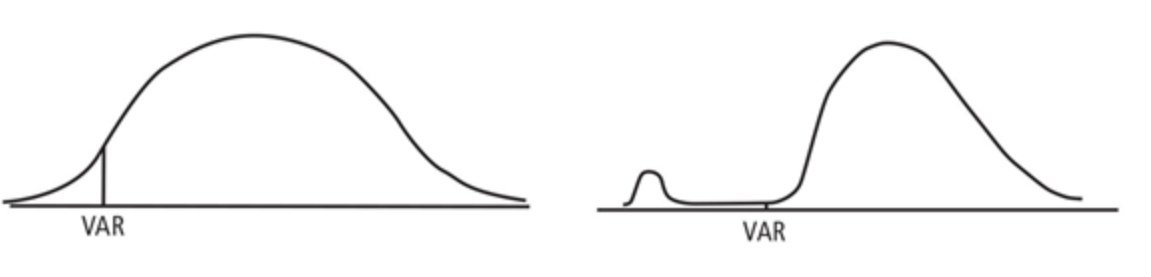
A diferencia del VaR, el CVaR o "Expected Shortfall" es la pérdida esperada una vez superamos el umbral de pérdidas máximas que nos ilustra el VaR. Podríamos decir que es un VaR del propio VaR.

A pesar de que en esta ilustración el VaR sería el mismo ya que ambas tienen la misma propoción de población, en la imagen de la derecha existiría mayor riesgo de impacto, pues los peores eventos están más concentrados. A raíz de esta problemática surge el CVaR, que nos indica la pérdida esperada para esa cola de distribución para la que el VaR no es suficiente. El uso del CVaR se ve justificado en determinados escenarios que puedan ser muy volátiles, aunque es mucho más limitante. 

Existen una serie de limitaciones intrínsecas al modelo que vale la pena considerar cuando queremos estimar esta medida en función de la metodología y de si la selección de los datos es a través de simulaciones, datos históricos, etc.. aunque algunas pueden paliarse:

• No determina pérdidas más allá del nivel de confianza estimado.
   
• Es una medida estática que puede variar en cuanto aumentamos la cantidad, calidad o ponderación de los datos que la conforman, es decir, a medida que avanzamos en el tiempo o cambiando el horizonte temporal, nuestra percepción de la distribución de resultados cambia. El horizonte temporal del cálculo debe ser escogido en base al tiempo que creamos que vamos a estar expuestos a ese riesgo con una determinada posición y activos. 
   
• El cálculo se basa en la distribución normal de los retornos, distribución de la que hemos hablado ya en otras ocasiones. La distribución normal presupone que cada retorno es independiente y fruto del azar, cosa que no es así, ni tampoco tiene en cuenta posibles deformaciones en las colas de la distribución o "fat tails". La distribución normal puede resultar válida para carteras amplias, bien diversficadas, pero no cuando puede existir una concentración de riesgos.

Parte de estas limitaciones se corrigen con el empleo del Stressed VaR y del Expected Shortfall o CVaR, un factor de decaimiento exponencial y de ajustes de valoración conservadores.

Actualmente existen 3 metodologías para el cálculo del VaR de una cartera, el método paramétrico o de correlación (que deberemos saber escoger muy bien el periodo a analizar), vía simulaciones históricas o simulaciones de Montecarlo, que permiten un gran abanico de posibilidades pero requiere de cierta potencia de cálculo para tener buenos resultados.

• El VaR paramétrico se estima a través del coeficiente de correlación que se presume constante y en base a los datos históricos de los activos para estimar la volatilidad (el periodo escogido será de vital importancia para unos resultados significativos), pero también podemos escoger periodos "específicos" si los consideramos más representativos, aunque podemos caer en sesgos de interpretación. Nutrir el modelo con buenos datos es esencial y necesario para poder tener un VaR del que nos podamos fiar.
   
• El VaR histórico tiene la ventaja de no necesitar correlaciones y no cae en las limitaciones de estas. Al usar una gran cantidad de datos históricos podemos incluir eventos de gran impacto y cisnes negros, pero también tenemos datos que pueden ser irrelevantes por su contexto histórico. 
   
• El VaR con Montecarlo es el más flexible y predice resultados a futuro con una volatilidad y correlación específicos. Se obtiene un mayor realismo de los resultados.

El Var también puede calcularse a través de las rentabilidades obtenidas y puede ser diferente si en nuestra cartera tenemos "cortos" con cierto carácter de permanencia.

Procedamos a analizar el código en detalle del siguiente ejemplo:

Primero debemos importar las librerías o cargar alguno de sus módulos. En este caso hacemos uso de pandas_datareader, numpy, y el método norm de scipy.stats.

from scipy.stats import norm
import matplotlib.pyplot as plt
import pandas as pd
import pandas_datareader.data as wb
import numpy as np

A continuación definimos una fórmula para trabajar con los datos de yahoo finance, como siempre, para poder tener los datos ajustados de cierre para cada uno de los valores que queramos, definidos en tickers, así como sus pesos relativos en tanto por uno en forma de matriz con np.array que usaremos más adelante. Generamos los retornos con data.pct_change().

Se muestra un ejemplo empezando el día 1 de enero hasta YTD:

La selección del periodo de retornos es vital a la hora de obtener un VaR significativo y del que podamos fiarnos.

tickers = ["AAPL", "FB"]      
pesos = np.array([.20,.80])            

data = wb.DataReader(tickers,"yahoo","2020-01-01")['Close']

returns = data.pct_change()[1:]

Calculamos las covarianzas entre los activos, la media de los retornos del periodo escogido (2020-1-1/YTD), la media ponderada por los pesos relativos de cada activo con .dot(pesos) y la desviación estándar del portafolio, que consiste en la raíz cuadrada de una multiplicación de matrices entre las covarianzas y los pesos relativos.

portfolio_mean = returns.mean().dot(pesos)
portfolio_stdev = np.sqrt(pesos.T.dot(returns.cov()).dot(pesos))

Escogemos el tamaño de la cartera con la variable investment y calculamos la media y la volatilidad ponderada por la inversión y añadimos el nivel de confianza en tanto por uno (99%/0.01-95%-0.05), etc...

El método norm.ppf() toma un porcentaje y devuelve un multiplicador de desviación estándar para el valor en el que ocurre ese porcentaje. Para una función de distribución calculamos la probabilidad de que la variable sea menor o igual que x para una x dada. Para la función de punto porcentual ppf(), comenzamos con la probabilidad y calculamos la x correspondiente para la distribución acumulativa.

Con num_days tendremos el número de días de los que queremos conocer el VaR. A mayor número de días mayor será la potencia de cálculo necesaria para obtener resultados, ten cuidado. A partir de ahí y con los datos necesarios para calcular el VaR, hacemos un bucle calculando para cada valor y día, multiplicando el VaR a 1 día , var_1d, por la raíz cuadrada del tiempo np.sqrt  y redondeando a 2 decimales, analizando también cómo ha variado el portfolio con el paso de los días.

investment = int(1000000)

mean_investment = (1+portfolio_mean) * investment
stdev_investment = investment * portfolio_stdev

conf_level = 0.05
cut = norm.ppf(conf_level, mean_investment, stdev_investment)

var_1d = investment - cut 

days = int(252)

print(("\nLa pérdida máxima de tu cartera inicial de " + str(investment) + 
    " usd con un nivel de confianza del " + str((1 - conf_level) * 100) + "% y para los siguientes " + str(days) + " días es de:\n"))

var_array = []

for i in range(1, days+1):
    var_array.append(np.round(var_1d * np.sqrt(i), 2))
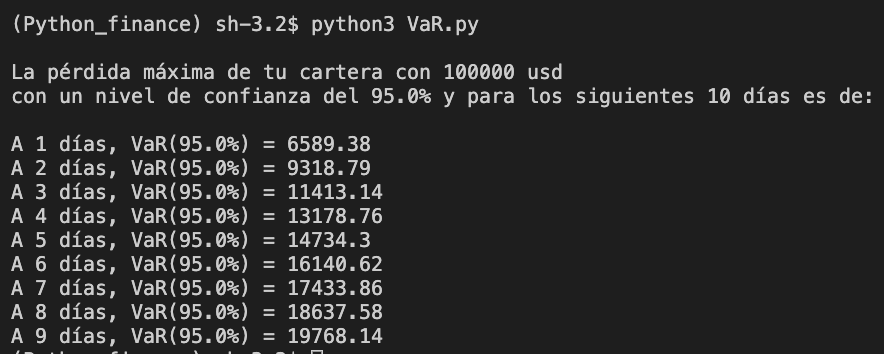
    print("A " + str(i) + " días, VaR(" + str((1 - conf_level) * 100) + "%) = " + str(((np.round(var_1d * np.sqrt(i), 2))))+ "   Portfolio : " +str((np.round(investment * (1+portfolio_mean)**(i),2 ))))

Representamos el gráfico con matplotlib y nos queda la curva que delimita la pérdida máxima para un nivel de confianza del 95% con el paso de los días. También podemos comprobar la distribución de retornos de cada activo de la cartera graficando con hist

plt.xlabel("Días")
plt.ylabel("Pérdida máxima de la cartera (USD)")
plt.title("Perdida máxima de la cartera para el periodo")
plt.plot(var_array,"r")

returns.hist(bins=60,histtype="stepfilled",alpha=0.5)

plt.show()

Aquí os muestro el script entero:

from scipy.stats import norm
import matplotlib.pyplot as plt
import pandas_datareader.data as wb
import numpy as np

tickers = ["AAPL", "FB"]      
pesos = np.array([.20,.80])            

data = wb.DataReader(tickers,"yahoo","2020-01-01")['Close']

returns = data.pct_change()[1:]

portfolio_mean = returns.mean().dot(pesos)
portfolio_stdev = np.sqrt(pesos.T.dot(returns.cov()).dot(pesos))

investment = int(1000000)

mean_investment = (1+portfolio_mean) * investment
stdev_investment = investment * portfolio_stdev

conf_level = 0.05
cut = norm.ppf(conf_level, mean_investment, stdev_investment)

var_1d = investment - cut 

days = int(252)

print(("\nLa pérdida máxima de tu cartera inicial de " + str(investment) + 
    " usd con un nivel de confianza del " + str((1 - conf_level) * 100) + "% y para los siguientes " + str(days) + " días es de:\n"))

var_array = []

for i in range(1, days+1):
    var_array.append(np.round(var_1d * np.sqrt(i), 2))
    print("A " + str(i) + " días, VaR(" + str((1 - conf_level) * 100) + "%) = " + str(((np.round(var_1d * np.sqrt(i), 2))))+ "   Portfolio : " +str((np.round(investment * (1+portfolio_mean)**(i),2 ))))

plt.xlabel("Días")
plt.ylabel("Pérdida máxima de la cartera (USD)")
plt.title("Pérdida máxima de la cartera para el periodo")
plt.plot(var_array,"r")

returns.hist(bins=50,histtype="stepfilled",alpha=0.5)
plt.show()