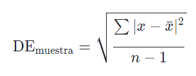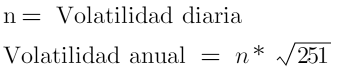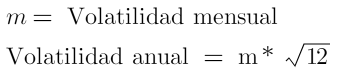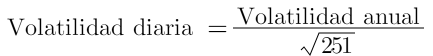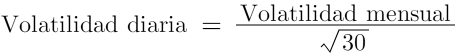Retornos, Riesgo y Volatilidad (Parte II)

El concepto de volatilidad aplicado a activos financieros generalmente se puede definir como la variabilidad de su tasa de rendimiento, generalmente anualizada. El problema viene a la hora de definir los indicadores con los que mediremos esta volatilidad. A menudo se usa la desviación típica, como mostramos en la parte 1.

Una desviación estándar de la media representa un intervalo de confianza del 68% de todas las observaciones dentro de la distribución media. Dos desviaciones representan el 95% de los casos. Tres desviaciones típicas representan el 99% de los datos.

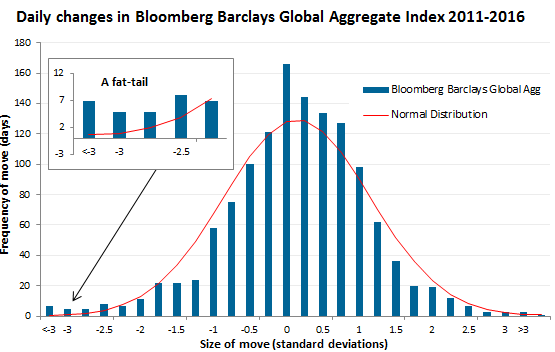
Este es el marco teórico, a la hora de analizar los rendimientos reales, las desviaciones a más de 3 sigmas se dan con mayor frecuencia de lo que la teoría sugiere. Al efectuar este ejercicio, se está suponiendo que el modelo teórico de valoración del activo es correcto y que el mercado forma expectativas de volatilidad utilizando eficientemente la información de que dispone. Ello hace que el precio de mercado resuma de manera adecuada toda la información disponible acerca del activo. La liquidez es otra pieza fundamental dentro del tema. Las empresas de mayor capitalización y free float (o blue chips) tienden a una volatilidad menor que empresas poco líquidas, entendiendo liquidez como la capacidad del activo de venderse sin cambiar significativamente el precio y con una pérdida mínima (la vivienda es menos líquida que las acciones)

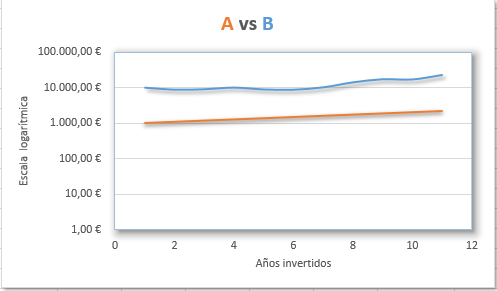
En el ejemplo siguiente podemos observar dos tipos de inversiones a lo largo de 10 años, sin tener en cuenta impuestos, dividendos, comisiones, ni entradas o retiradas de capital para simplificar.

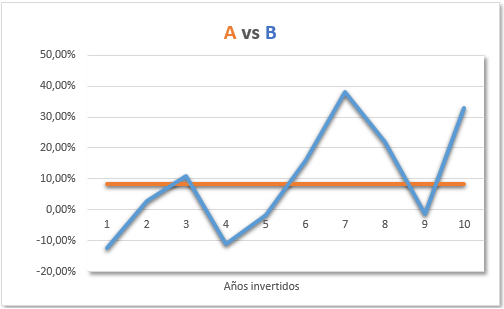
Numéricamente y analizando las variaciones en el capital, la inversión A no ha sido volátil, ya que la rentabilidad anual en este caso coincide con la rentabilidad media. Sin embargo sí hay volatilidad en la inversión B. En este caso, la escala lineal nos ayuda a apreciar visualmente las variaciones en precio partiendo de capitales dispares si lo analizamos a partir del capital invertido.

Analizando las variaciones en las rentabilidades sí nos damos cuenta de la diferencia. A pesar de ser una inversión altamente volátil comparada con A, la inversión B es mejor en términos porcentuales.

Siguiendo con el ejemplo, podemos calcular la desviación estándar de las rentabilidades anuales de la inversión “B”. En Excel esta fórmula se encuentra con la forma “=STDEV()” o “=DESVEST()", concretamente se refiere a la desviación de muestra (n-1) y no población (n) en el denominador. Aquí tienes el cálculo hecho a mano.

Volatilidad_{10 años} = 17, 45%

En ejemplos sencillos como estos la desviación estándar funciona muy bien, aún más si tenemos en cuenta que todos los datos ya estaban anualizados. La volatilidad histórica se calcula a partir de la desviación y a través de series temporales como veremos más adelante.

Para poder hacer el cálculo de la desviación, primero debemos tener todos los datos de rentabilidad en una misma medida temporal. Para anualizar la volatilidad debemos multiplicar el dato de la rentabilidad por la raíz cuadrada y el número de periodos escogido. La volatilidad no se incrementa en la misma proporción que la rentabilidad sino que crece como la raíz cuadrada del tiempo. La selección de datos a partir del precio suele hacerse con los de cierre diarios, o algún dato relevante, lo importante es que estemos comparando lo mismo. En cuyo caso 251 o 252 sería el número de días de trading posibles en un año, con esto anualizaríamos el dato diario, fácilmente podemos anualizar datos mensuales multiplicando por 12. En cambio para hacer diario un dato de volatilidad anual deberíamos dividirlo.

El problema surge cuando las cosas comienzan a complicarse.

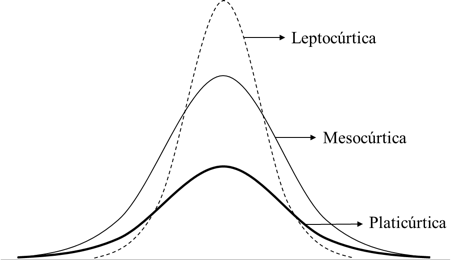
La no-normalidad en las distribuciones son habituales en series financieras: Aparecen los conceptos de skewness y curtosis (“fat tails”). La forma de la distribución en los retornos no sigue del todo una distribución normal. Dependiendo de lo que midamos, la distribución suele ser más plana, alargada, inclinada hacia algún lado, o con más valores en los extremos de lo que 3 desviaciones estándar prevén (99,7% de posibilidades según modelo).

Se suelen clasificar 4 propiedades estadísticas presentes en muchas de las observaciones de rentabilidades en activos financieros: clúster de volatilidad (parte 1), asimetría en los retornos, persistencia y no linealidad.

Se denomina clúster de volatilidad al hecho de que los días de volatilidad superior a la media suelen estar agrupados, se observan días de gran intensidad tanto a la baja como al alza, seguidos de días con baja volatilidad, (de ahí la formación de tendencias).

La asimetría en los retornos, tan presente en mercados de renta variable hoy día, concluyen que el impacto en los retornos que tiene la volatilidad en episodios bajistas es más fuerte que en los alcistas. La dependencia no lineal la encontramos en cómo precios de diferentes activos se mueven de forma independiente la mayor parte del tiempo, pero en etapas de crisis o bonanza se correlacionan y mueven en una misma dirección.

En la práctica, estos eventos extremos tienen más probabilidad de ocurrencia que los que pueden predecir los modelos normales y las dependencias lineales, los cubren los modelos de volatilidad multivariables o estocásticos como el ARCH/GARCH y derivados, siempre que partamos de la base de que no existe correlación en los retornos. Una cuarta propiedad fácilmente observable es la reversión a la media, la experiencia empírica nos dice que la volatilidad siempre revierte a su media de largo plazo.

Volatilidad implícita vs Volatilidad histórica:

Se denomina volatilidad implícita a la perspectiva de los inversores con respecto a un activo. No hay garantía alguna de que se cumpla, se trata de probabilidad. Esta volatilidad implícita viene dada por los precios que se observan en el mercado de derivados que cotizan en volatilidad, como las opciones Call y Put, entre otros. 

La Vol.Implícita se extrae de la ecuación que determina el precio teórico del derivado comparándolo con el observado en el mercado (fórmula Black Scholes). Al efectuar este ejercicio, se está suponiendo que el modelo teórico de valoración del activo es correcto (Black-Scholes generalmente), y que el mercado forma expectativas de volatilidad utilizando eficientemente la información de que dispone. Ello hace que el precio de mercado resuma de manera adecuada toda la información disponible acerca del activo. 


Modelo Black-Scholes:

Es un modelo teórico para determinar el precio de opciones financieras. El modelo tiene limitaciones, ya que supone también contratos de opciones que expiran a vencimiento (no tradeables como en mercado americano, también llamadas opciones europeas), distribución normal en los retornos, sin dividendos ni costes de transacción o impuestos, y sin posibilidades de arbitraje, etc... pero es un modelo muy utilizado y se ha ganado su fama a pulso.

Con este proceso podremos determinar si existe infravaloración o sobrevaloración de una opción en base a si la volatilidad cotizada es superior o inferior a la implícita y generar estrategias en torno a esto: ponerse corto o largo en volatilidad, por ejemplo (comprar o vender opciones). Cambios en la información disponible (resultados de una empresa, noticias inesperadas, intervenciones de política económica) afectan a su variación.

La griega vega(γ) de las opciones mide la tasa de cambio de su valor con respecto a la volatilidad. Un trader que quiera cubrir una posición contra los cambios de esa volatilidad, realizará una estrategia "vega neutral", tomaría una posición compensatoria para anularla, esto evitaría que cambios en la Vol. Implícita afecten a su cartera o posición, aunque si variaciones en las demás griegas.

Una posible estrategia es poder comparar el spread (diferencia) entre la volatilidad implícita y la histórica para cada subyacente y ver si ésta cotiza por encima o por debajo, sin olvidar que ninguna estrategia es infalible por si sola y merece ser contrastada desde otras perspectivas. Es interesante también analizar volumenes y capital negociado de subyacentes por periodos de vencimiento para tratar de detectar movimientos así como UOA (Unusual options activity).

La volatilidad histórica se basa exclusivamente en el pasado mientras que la implícita mira hacia el futuro, tratando de estimar una característica no observable, sus cálculos difieren por completo, ya que la histórica se puede conseguir a través de la desviación típica obviando cualquier modelo de valoración.

En BarChart podemos encontrar screeners para analizar listas de activos. Por ejemplo existe este con el que podemos ver los activos más volátiles, tanto al alza como a la baja, en base a los filtros que nosotros queramos (tiempo, mercados, capitalización, sector...), también otro con la implícita de las opciones.